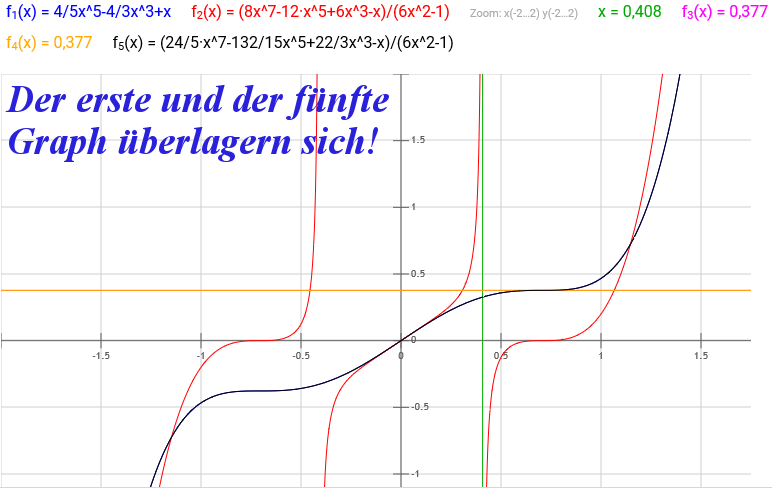
Integration einer Funktion unter Verwendung der 1. und 2. Ableitung:

folgendes Integral soll mit Hilfe der 1. und 2. Ableitung einer Funktion berechnet werden:

Integral (4x^4-4x^2+1)dx=4/5x^5-4/3x^3+x=F(x)

folgender Ansatz, den ich beim erfolglosen Berechnen des Gaußschen Fehlerintegrals unter zu Hilfenahme einer binomischen Gleichung ermittelt habe, soll gelten:

f(x)*f'(x)/f''(x)=(16x^3-8x)/(48x^2-8)*(4x^4-4x^2+1)=(8x^7-12x^5+6x^3-x)/(6x^2-1)

es soll gelten: F(x)=4/5x^5-4/3x^3+x=(a*8x^7-b*12x^5+c*6x^3-dx)/(6x^2-1)

(6x^2-1)*(4/5x^5-4/3x^3+x)=(a*8x^7-b*12x^5+c*6x^3-dx), Koeffizientenvergleich ergibt:

x^7: a=24/40, x^5:b=132/180; x^3:c=22/18; x:d=1, diese konstante Faktoren werden gesucht

f(x)*f'(x)/f''(x)*s(a,b,c,d)=F(x) Ableitung bilden und die konstanten Faktoren ermitteln, wieder durch einen Koeffizientenvergleich

s(a,b,c,d)*((f(x)*f'(x)/f''(x))'=f(x)

a=(144x^8)/(240x^8)=12/20

b=(192-56a)x^6/(216x^6)=132/180

c=-(60b-88)x^4/(36x^4)=22/18

d=1

Damit wurde eine alternative Integralberechnung aufgezeigt. Vielleicht sind damit ja auch komplizierte Integrale berechenbar, für eine Beurteilung dieser Frage wäre ich dankbar! Das Gaußsche Fehlerintegral mit dieser Methode zu berechnen funktioniert leider nicht, da habe ich mich getäuscht!

weiterführende Berechnungen für die Integration bei s(x)

Berechnung der Funktion f(x) mit der Kettenregel und der ersten und zweiten Ableitung:

f'(f'(x))*f''(x)=(f(f'(x)))'

Beispiel: f'(x)=k*x^g     f''(x)=k*g*x^(g-1)    f(x)=k/(g+1)*x^(g+1) und f'(f'(x))=k*k^g*x^gg

f'(f'(x))=1/f''(x)*(f(f'(x)))'

f'(f'(x))=1/(k*g)*x^(1-g)*(k*k^(g+1)*1/(g+1)*x^g*(g+1))'=k*k^g*x^gg

k^(g+1)*x^gg=k*k^g*x^gg

Bestimmung von f(x):

f'(f'(x))*f''(x)=k²*k^g*g*x^(gg+g-1)=(f(f'(x)))'

Integral f'(f'(x))*f''(x) dx=k²*k^g*g/(g*g+g)*x^(gg+g)=f(f'(x₁))

f'(x₁)=k*x^g, daraus folgt: x₂=k*x₁^g     x₁=(x₂^1/g*k^-1/g)=a

k²*k^g*g/(g*g+g)*x^(gg+g)=k²*k^g*1/(g+1)*x₂^(gg+g)

daraus folgt: f(x)=k²*k^g*1/(g+1)*a^(gg+g)=k²*k^g*1/(1+g)*k^(-g-1)*x₁^(g+1)

f(x₁)=k/(g+1)*x₁^(g+1)

Es soll durch das Anlegen einer Funktion in der Krümmung einer Ausgangsfunktion, eine Komposition, die Ausgangsfunktion bestimmt werden…, eine andere Form einer Integration also.....!

Problem/Ansatz:

f(x)=x^n    f'(x)=n*x^(n-1)   f''(x)=n*(n-1)*x^(n-2)

Krümmung k=f''/(1+f'^2)^(3/2)

                  k=n*(n-1)*x^(n-2)/(1+n^2*x^(2n-2))^(3/2)

                  k^(-1)=(1+n^2*x^(2n-2))^(3/2)/(n*(n-1)*x^(n-2)), der einfacheren Rechnung halber.....

es soll gelten k^(-1)(g(x))=x^n

x^n=(1+n^2*x(g)^(2n-2))^(3/2)/(n*(n-1)*(x(g))^(n-2))

((n^2-n)*x^n)^(2/3)*(x(g))^(2/3*(n-2))=1+n^2*(x(g))^(2n-2)

((n^2-n)*x^n)^(2/3)=(x(g))^(-2/3n+4/3)+n^2*(x(g))^(4/3n-2/3)

Beispiel: n=2, daraus folgt: 2^(2/3)*x^(4/3)=1+4*(x(g))^2

+-(1/4*2^(2/3)*x^(4/3)-1/4)^(1/2)=x(g)=g(x), etwas unglücklich gewählt, die Variablen....

Probe: f(x)=k^(-1)=(2/(1+4x^2)^(3/2))^(-1), siehe weiter oben, n war bei diesem Beispiel ja 2

f(g(x))=x^n=x^2, richtig!!!!!!

habe dies für n=5 durchführen wollen, erhalte da ein sehr umfangreiches, nicht lösbares Gleichungssystem.....

n=5,x^5, daraus folgt: (20*x^5)^(2/3)=(x(g))^(-2)+25*(x(g))^6

25x^6+x^(-2)-(20*a^5)^(2/3)=0       x=....a=g(x), zu umfangreich, nicht lösbar......